How To Strengthen The Predictive Power of Your Marketing Mix Model
The biggest challenge when building a Marketing Mix Model is to ensure that it is robust enough to generate strong predictive power.
Model Validation is the overall process of comparing the model and its behavior to the real environment; it can be broadly split into two types: In-sample, and Out-of-sample validation. The latter is itself divided into two main types of validation, one of which is Cross-validation
This blog is a dive into the advantages and disadvantages of the concept: Cross-validation, as well as the context in which it is used. The first part of the blog briefly explores In-sample and Bootstrap Validation, while the second part is dedicated to examining the three main types of Cross-validation: Exhaustive, Non-exhaustive, and Time-series.
In-Sample Validation
This method is also known as “Goodness of Fit”. It is a way to measure how robust the model is, and how well it fits the data on which it was trained. To translate its evaluation into measurable values, in-sample validation uses metrics like Student Test/ F: Fisher Test/Durbin Watson/VIF: Variance Inflation Factor/ R²: the coefficient of determination/ Adjusted R²/Standard Error.
Out-of-sample validation:
Out-of-sample Validation evaluates how well a model predicts results for a new, unseen, set of data. In general, it consists of building the model on a subsection of the data: the training set. Once the model is created, it is then tested on a different set of data, which was not used to build it initially. This is called the Validation or Hold-out data set. Out of the two types of out-of-sample data, which are Bootstrap and Cross-validation, Cross-validation is more commonly used.
Bootstrap Validation:
Before delving into the details of Cross-validation, let’s recap the other component of Out-of-sample Validation. The Bootstrap method is a resampling technique (with replacement) used in applied machine learning.
Its purpose is to estimate the skill of machine learning models when making predictions about data that was not included in the training data. Bootstrap is useful when the analyst has a large sample size and when confidence intervals are needed.
We should mention here that confidence intervals are an attribute of Bootstrap that is not readily available with other methods such as Cross-validation.
To apply the bootstrap method, the analyst should follow this process:
1. Choose the number of bootstrap samples to perform.
2. Choose a sample size.
3. For each bootstrap sample:
a. Draw a sample with replacement, with the chosen size
b. Fit a model on the data sample
c. Estimate the skill of the model on the out-of-bag sample
4. Calculate the mean of the sample of model skill estimates.
Cross-validation:
The idea behind Cross-validation is to keep aside a portion of the data that the analyst will not use to train the model. That portion is later used to test/validate the model. Unlike Bootstrap, Cross-validation resamples without replacement. Thus, it produces surrogate data sets that are smaller than the original. Several Cross-validation techniques exist, and they could be classified into three categories:
Non-exhaustive Methods:
Holdout:
This is the most basic and the simplest non-exhaustive approach. The analyst just needs to divide the data set into two parts: training and testing. One of the main issues of this approach is instability, in that, it gives different results each time the analyst trains the model. Another issue is information loss. It could also lead to choosing a non-representative training set.
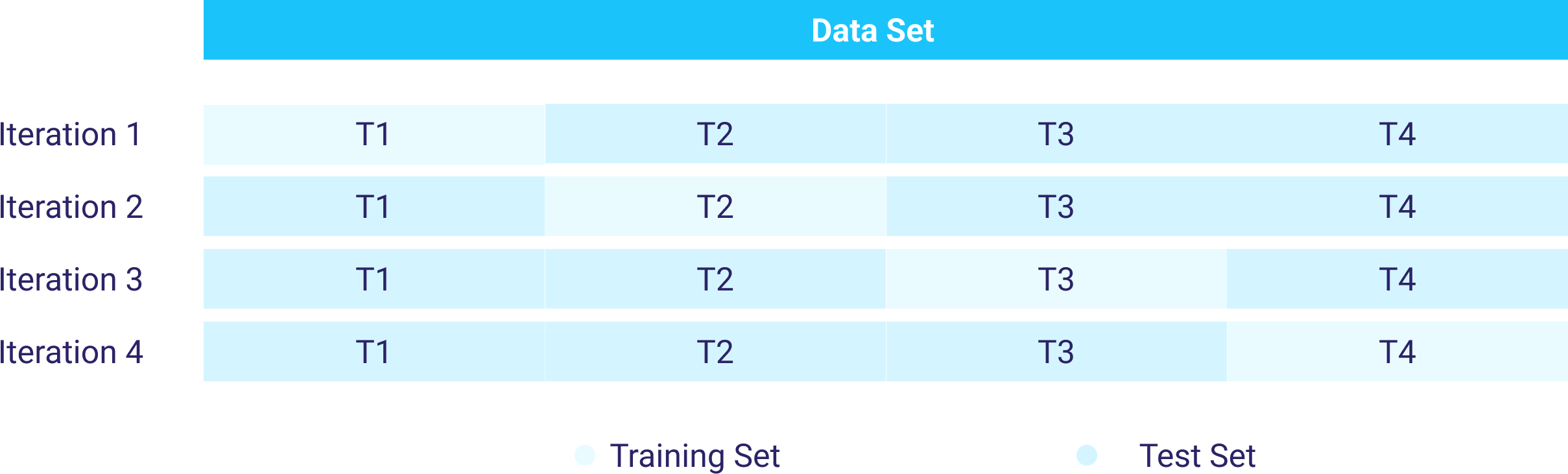
K-Fold Cross-validation:
This approach is a way of improving the Holdout method as it guarantees that the accuracy score doesn’t depend on the way data is split. The data set is divided into k number of subsets and the Holdout method is repeated k times, as illustrated in the graph below. On the positive side, K-Fold results in more accurate evaluation in comparison to Holdout. However, it is time consuming and produces highly imbalanced folds since the data is randomly .
Stratified K-fold Cross-Validation:
This method solves the issue of imbalanced training sets through creating stratified folds. Stratification is the process of rearranging the data while ensuring that each fold is a good representative of the entire set.
Exhaustive Methods
This component is made out of Leave-P-Out Cross-validation (LPOCV), and a simpler version of it called: Leave-one-out Cross-validation (where p = 1). The latter is deployed when the data set is small and when the model accuracy is more important than the computation cost.
When using the LPOCV, however, the analyst retrieves p observations out of the dataset. They, train the model on n-p observation and test it on the p points. This process is repeated for all possible combinations of p from the dataset. The final accuracy is the average of all the iterations. The problem with this method is that it’s time consuming, because the higher the value of p, the more combinations there is.
Time Series Cross Validation:
Traditional Cross-Validation methods are not appropriate in the case of Time Series Data. This is due to a high dependency on time; the need to respect the flow of the chronological events; and the fact that data random split is invalid in the context of time series. In this section of Cross-validation, we distinguish 3 subcategories:
- Cross-Validation on Rolling Basis:
In this type of Cross-validation, the analyst should start with a small subset of data for training purposes, forecast for the later data points, and then check their accuracy. The same forecasted data points are then included as part of the next training dataset, and subsequent data points are forecasted.
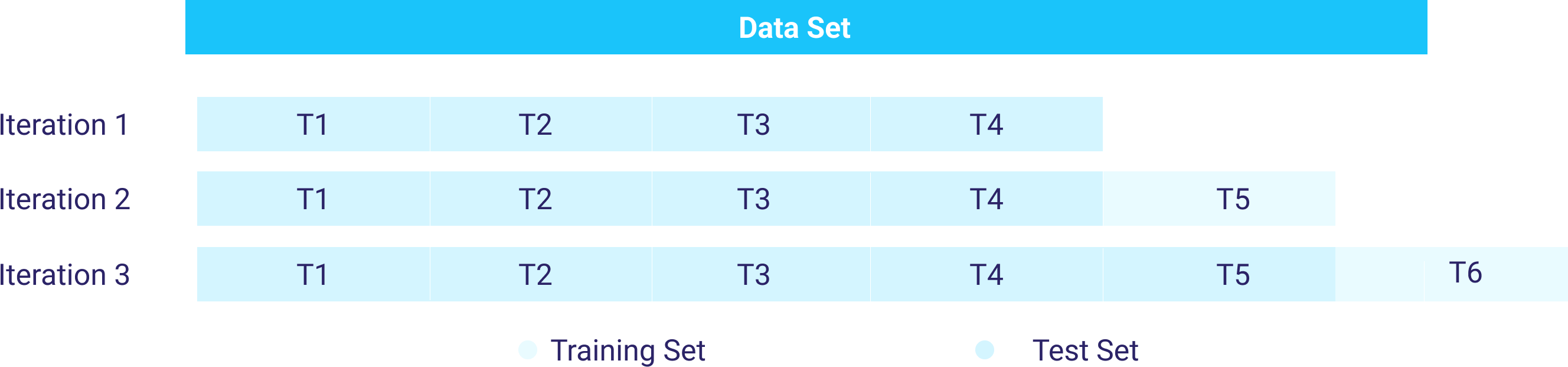
This method deals with an arbitrary choice of test sets by running multiple splits. However, it can generate biased estimations as well as leakage from future data.
- Blocked Cross-Validation:
This method works by dividing the dataset into folds and by removing blocks of size h from either side of testing folds to block potential information leakage of dependent points. This also helps reduce the temporal dependency between observations. However, it can be computationally expensive when having a large dataset.
- Nested Cross-Validation:
It is composed of an inner loop that functions as a training and validation set, and an outer loop that encompasses the inner loop and the test set. Nested Cross-validation gives the best parameters estimation and protects against overfitting. But it is time-consuming and very costly.
Conclusion
Model Validation is a crucial step to ensure the robustness of the marketing mix model and the generalization of the obtained results. In-sample and Out-of-sample validation are the main methods of Validation, with Out-of-sample Validation being the method with multiple options to choose from. Regardless of the choice of the validation technique, marketing mix modeling analysts should always remember that it is an essential part of the Modeling phase, referring to the Marketing Mix Modeling Workflow. In fact it draws its importance from being a crucial step towards ensuring that the client receives the right recommendation when it comes to the course of action to take in the future. To put it simply, Prediction is built on the analysis of historical data and its accuracy depends on the robustness of the measurement, which can only be achieved when Validation is carried out properly.