Regression Analysis
for Marketing Mix Modeling
This comprehensive guide will give you an overview of what regression analysis is, its different types and how it can be leveraged in Marketing Mix Modeling.
Regression analysis is an important part of model building, the fourth phase in the MMM workflow. It is a powerful approach used to uncover and measure the relationship between a set of variables and a specified KPI, and predict future outcomes. This makes it a very useful and common technique in building marketing mix models.

Regression analysis has prescriptive power and is often used to predict the value of a variable (the dependent variable/ the KPI of interest), based on other variables (the independent variables).
By the end of this blog, you will be well-versed in the basics of regression analysis and ready to start making data-driven decisions by interpreting the results of your regression analysis.
Let’s start first by defining a key component of regression analysis.
WHY IS CORRELATION CRUCIAL FOR REGRESSION ANALYSIS?
Correlation – Also called Pearson’s Coefficient of Correlation – is a key statistic that needs be computed and analyzed as part of the explore phase of the MMM workflow.
This metric is useful to appreciate the strength of the relationship between two variables. However, the presence of a correlation does not necessarily mean causality. Possible explanations include:
• Direct cause and effect: water causes plants to grow
• Both cause and effects: coffee consumption causes nervousness; nervous people have more coffee.
• Relationship caused by third variable: death due to drowning and soft drink consumption during summer. Both variables here are related to heat and humidity (third variable).
• Coincidental relationship: an increase in the number of people exercising and an increase in the number of people committing crimes.
Pearson’s Correlation coefficient
is a standardized covariance:
r=\frac{cov(x,y)}{\sqrt{var(x)}\sqrt{var(y)}}
• Measures the relative strength of the linear relationship between two variables
• Unit-less
• Ranges between -1 and 1
• The closer to -1, the stronger the negative linear relationship
• The closer to 1, the stronger the positive linear relationship
• The closer to 0, the weaker any positive linear relationship
As mentioned before in this article, Correlation is a key component to be calculated and analyzed as part of the MMM workflow. However, it is important to mention that it can only depict linear association and it fails to depict any non-linear associations.
THE SIMPLE LINEAR
REGRESSION
What is the impact of advertising on sales? Or in other terms, if you know how much budget you are investing in advertising, are you capable of forecasting how much sales you can achieve ? Regression analysis allows you to do that!
But before dealing with real-life examples that require elaborate types of Regression, let’s use the Simple Linear Regression to fully understand how the process works.
First, you need to collect a sample of data periods about x, in this case, the advertising spend; and a sample of data periods about y, in this case, the sales volume. Then, you use the regression technique to estimate the relationship between the variations period on period of advertising and the variations in sales. Statistically speaking this means estimating the coefficients \beta _{0} and \beta _{1}. Once these are estimated, then you can discover the level of sales that could be achieved when a specific advertising spend is deployed.
Now that we got the business element explained, let’s dive into the mathematical side of the simple linear regression:
The equation of a simple linear regression depicts a dependency relationship between two variables or two sets of variables. The first set is called the dependent variable, and the second set would be the predictors or independent/explanatory variables. Given that this is “simple” linear regression, the independent variables set is composed of only one variable. This variable is used to predict the outcome of the dependent variable.
To predict the outcome for different values (or scenarios of x, the analyst needs to estimate β0 and β1 from the data collected.
y=\beta _{0}+\beta _{1}+\varepsilon
y = Dependent Variable
x= Independent Variable
β0 = Intercept
β1 = Slope
ε = Error term
ε ≈ Normal Random Variable with E(ε) = 0 and V(ε) = σ², i.e ε ~ N (0,σ²)
E(y/x) = \beta _{0} + \beta _{1} x

Parameters
• β0 and β1 are unknown, and the goal is to estimate them using the data sample.
• β0 is the base.
• β1 represents the coefficient of the independent variable x.
• ε is the error term or residual. In regression analysis, it is important that the error term is random and is not influenced by any other factor. It should be as small and as random as possible.
a.
HOW DOES LINEAR REGRESSION WORK?
Let’s consider the following equation that models the impact of advertising on sales.
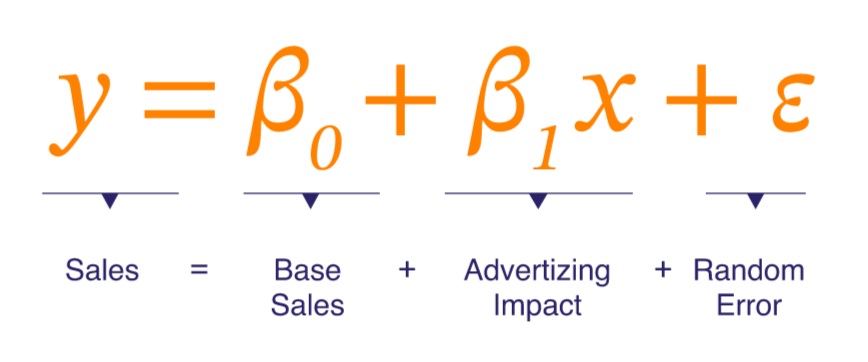
\underbrace {y}_{Sales} = \underbrace {\beta_{0}}_{Base Sales}+\underbrace {\beta_{1}x}_{Advertising Impact}+\underbrace {\varepsilon}_{Random Error}
When data is plotted, we obtain the following chart where each point has an x coordinate and y coordinate:
• x represents the advertising budget.
• y coordinates represent the sales that have been achieved for a particular advertising spend (value of x).
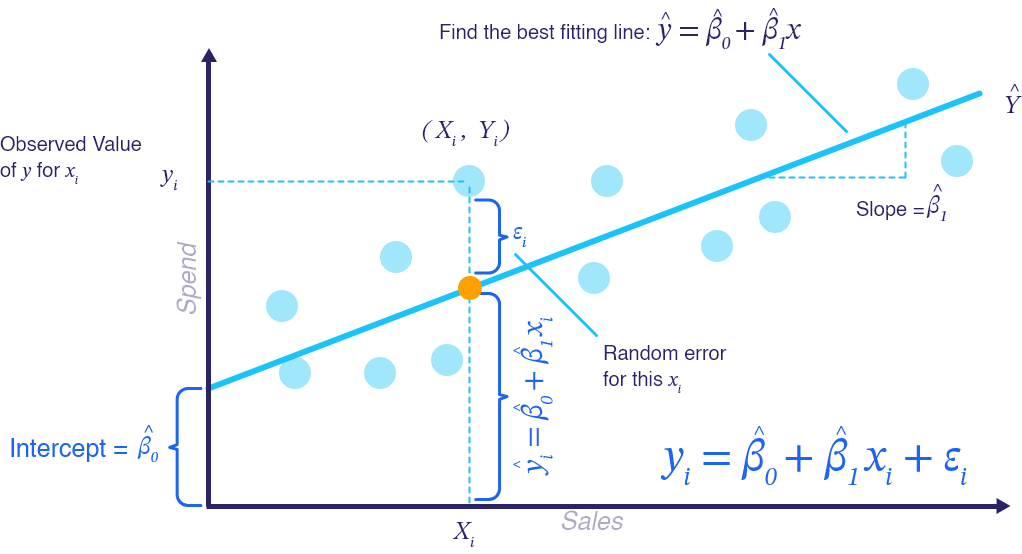
The goal of the simple regression analysis is to find the line (i.e. the intercept and slope) that goes through the maximum data points in this chart, minimizing the distance between each point and its projection on the “searched for” line.
The blue line is the best line and is the estimate or \widehat{y}. Point estimates are obtained by projecting the initial data points (the dots) on the estimate line \widehat{y}.
The fitted line equation is : \hat{Y}=\hat{\beta _{0}}+\hat{\beta _{1}}x. → Note here that it is no longer about β0 and β1, but rather their hat variations, because the parameters β0 and β1are being estimated using \hat{\beta _{0}} and \hat{\beta _{1}} based on the sample of data collected.
The intercept is where the blue line intercepts the y-axis. That represents the base sales.
The slope is that of the curve of the fitted line. Any data point is represented by two coordinates x, y. Any projected point on the line will result in its estimate \hat{y}.
The difference between the initial position of the point and its projection on the line, which is represented by the dot in orange, represents the error term. The smaller the value of the error term, the better is the regression line in estimating the relationship between x and y.
OLS: Ordinary Least Squares is the method that is used to estimate the parameters β0 and β1 and to minimize the error term.
b.
HOW REFINED COULD
YOUR FORECAST WITH REGRESSION ANALYSIS BE?

To estimate the volume of sales to be achieved in a given period, a simple method consists in quoting the average sales of the previous periods; in other terms, use a simple forecasting method based on the average. On the other hand, if regression is used, the forecast is a little more sophisticated.
In regression analysis, the concept we try to illustrate is that when we know how much budget is to be deployed for adverting, this information about the “independent variable” can be used to refine the forecast about the sales to be achieved. Presumably a forecast based on regression should be superior to the forecast based on the simple average method!
How much prediction improvement is achieved when using regression over the simple average method? This leads us to introduce the concept of variance decomposition. The aim is to achieve a decomposition of the total variance SST (sum of squared total) into two components:
1.
What is explained by the model (the regression line), which is represented by SSR.
2.
The residual part (the unexplained part) of the equation, which is SSE: The Sum of Squared Error.
Total variation consists of two parts
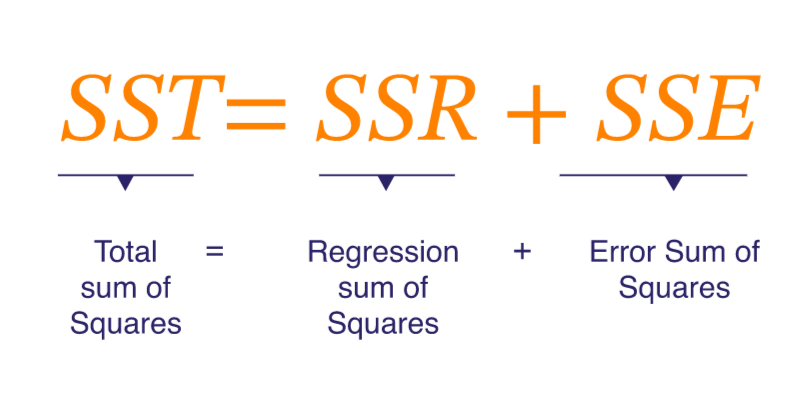
In the following chart:
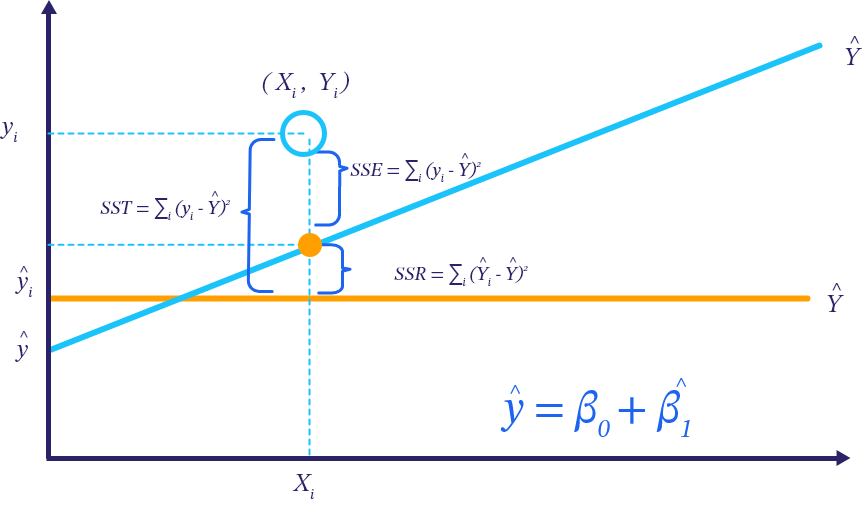
The projection of a specific point on the blue line represents the estimate \hat{y}.
The difference between the estimate and the yellow line represents what would be gained when using regression to do the forecasting (over the simple average method).
The difference between the real point, which is the red point in the graph, and its projection on the yellow curve, represents what is called the error, or the residual.
The ideal situation is one where the sum of squared error (the residual) is very small compared to the SSR, which is the sum of squared regression.
c.
HOW MUCH VARIANCE
IS EXPLAINED BY
THE MODEL? R-SQUARED (R²)
Those who are familiar with Regression or Marketing Mix Models have certainly heard about R² multiple times! But what does it really mean in Layman’s terms?
What is explained by the model (the regression line), which is represented by SSR.
R^{^{2}}=\frac{SSR}{SST}, where: 0\leq R \leq 1
R² simply represents the portion of the variance in the dependent variable that is explained by the model or the independent variable. The higher the R² the better In our sales/advertising example, if R² equals 70 %, it would mean that 70% of the variation in the sales data is explained by the movements in the advertising variable. So, advertising can explain 70% of the variation in the dependent variable (sales).
R² is a very important metric in Marketing Mix Models as it gives an indication of how successful the model, and its variables, are in explaining the variations in the modeled KPI.
d.
HOW ACCURATE IS YOUR MODEL?
THE STANDARD ERROR OF
THE ESTIMATE (SEE)
This is a measure of the accuracy of the model. It is simply the average of the error term (difference between the real y values and their estimate \hat{y} ). This statistic is very useful as it shows how accurate the results of the modeling are and the prediction power of the model.
TIP:
Analyze your residuals and plot them at all times! Make sure the OLS assumptions are respected and use the relevant statistics to establish your assessment (DW, VIF, Normality test, homoscedasticity etc.).
e.
HOW RELIABLE IS YOUR MODEL?
THE T-STAT

The t-stat is a standard output of the model and a very important statistic to look at when building MMM models. Remember that the dataset used to create a regression model is a sample. That sample is used to estimate the parameters β0 and β1 at the population level. It is therefore very important to ensure that the estimates we obtain from the sample are reliable and are good estimates for the population parameters. In other terms, if we had picked up another sample from the same population, would have we obtained the same estimates (within a certain confidence interval)? That is exactly what the t-stat is for.
As a rule of thumb, the t-stat should be above 2 to make sure that we are reporting reliable impacts.
f.
What Does Real-life
Regression look like?
Now that you explored how Simple Linear Regression works, it’s time to move to what happens in real life when working on an MMM project.
There are many variations of Regression analysis that are used in Marketing Mix Modeling:

In this part of the article, we’re going to discuss the Multiple Linear Regression. If you’d like to learn about the other types, check out the following article.
Multiple
Regression
Multiple Regression is as simple as stating that the period on period movements/variations in the dependent variable (the KPI that we are interested in modeling, e.g. sales) are not any more explained by the variations of the movements of one single variable, but rather by the movement of multiple variables.
This is of course a more representative setting as simple linear regression is hardly used in real life MMM projects; as it is too simplistic and does not handle the complexity of consumer behavior and the media landscape.
Thus, when the analyst starts adding more variables into the regression equation, they move from simple regression setting to multiple regression setting.
In a typical marketing mix modeling project, multiple variables impact the sales performance, e.g.





To be able to measure the impact of those variables on sales or any other chosen KPI, the analyst needs to build a robust model which accounts for all the variables influencing the movement of sales.
y=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\beta _{3}x_{3}+\beta _{4}x_{4}+...+\beta _{k}x_{k}
- \beta _{0},\beta _{1},...,\beta _{k}: are population model parameters (coefficients) to be estimated from the sample.
- \beta _{0} represents the base, a very important concept in MMM.
- x _{1},x _{2},...,x _{k} are the independent variables influencing sales.
- The term \beta _{k}x_{k} represents the contribution of the variable x_{k} on sales: i.e. how much sales are driven by the variable x_{k} (incremental impact)
- \varepsilon : are the error terms, assumed to be independent and following the normal distribution with 0 mean and constant variance.

Estimating this model will help the business better predict their sales performance. In that, they gain insights into:
- The impact of every media channel on sales be it online or offline.
- The budget they should allocate to media before reaching saturation.
- The promotional mechanics they should utilize.
- The distribution levels to be maintained.
- How seasonality could be leveraged.
Once they estimate the parameters, \beta _{0},\beta _{1},...,and \beta _{k}, are estimated they can easily plug in the values to any media and marketing scenario hey have been given and to predict the incremental sales they will make. This becomes a powerful tool for decision making.
a.
HOW THE PARAMETERS
ARE ESTIMATED
The process is the same as that of the simple linear regression. The goal is to minimize the residuals, which is the difference between y and \widehat{y}. The method of estimation is also the same, which is the Ordinary Least Squares (OLS) method that consists in finding the estimates of \beta _{0},\beta _{1},\beta _{2}..., and \beta _{4} that minimize the sum of the squared error:
\sum_{i=1}^{n}(y _{i}-\hat{y _{i}})^{2}
b.
COEFFICIENT
INTERPRETATION
In a given equation, the estimated coefficient \widehat{\beta _{k}} related to the advertising variable x _{k} would represent the sensitivity of the dependent variable to variations in the independent variable x _{k}.
In a given equation, the estimated coefficient \widehat{\beta _{k}} related to the variable x_{k} represents the sensitivity of the dependent variable to variations in the independent variable x_{k}.
For instance, if x_{k} represents the search activity expressed in terms of millions of impression, then we estimate that 1 unit movement in x_{k} (i.e. 1 Million impression) will yield \widehat{\beta _{k}} units increase in sales, while keeping all the other variables in the equation (seasonality, promotions, distribution, etc…) at the same level.
The coefficient in the context of multiple regression is also commonly called a partial correlation coefficient because it explains how much the dependent variable will move as a result of the movement of an independent variable while keeping all the other variables at the same level.
TIP
When estimating the coefficients in the context of multiple regression, you need to make sure they are reliable so you can interpret them. To check this, compute the t- stat associated to each coefficient.
Conclusion
You now know how to conduct a regression analysis for your marketing mix modeling project. But it doesn’t end there, there are other modeling techniques we didn’t cover, like other types of linear regression, as well as non-linear regression!