Using Pooled Regression
to Model Different Regions in MMM
Using Pooled Regression
to Model Different Regions in MMM
Previously, we have explored the Return on Investment for Marketing Mix Modeling. In this article, we cover Pooled Regression, an advanced modeling technique used when you need granular measurement at different levels.
When building Marketing Mix Models at the national level, sales are modeled altogether (total sales). There is no interest in analyzing the details of, for example, where certain sales come from. However, if the model is created at the regional level, those details become crucial.

For example, a retailer wants to understand their sales variation store by store. Similarly, a CPG brand might be interested in analyzing the variation of sales by region. In these situations, Pooled Regression would be needed.
What is Pooled Regression?
Pooled Regression, also known as panel regression, is a statistical method used to analyze data that has both cross-sectional and time-series dimensions.
It combines the advantages of cross-sectional analysis (examining differences among different entities at a specific time) and time-series analysis (examining changes within the same entities over time).
By pooling the data together, the analyst can gain a more comprehensive understanding of the relationships between variables across sections and across periods.
What is a Cross-Section?
A Designated Market Area (DMA)
Los Angeles, Dallas Washington, Philadelphia…
A Media Region
BARB TV Region…
A Store
Walmart Green Mall, Walmart North Bergen…
A Retailer
Walmart, Walgreen, Costco, Target …
A Sub-Product
Pack size, Flavor …
A Specific Aggregation
Multiple Grocery Stores Vs Pharmacy Stores…
- Pooled regression is commonly used in econometrics and can be estimated using techniques such as ordinary least squares (OLS).
Benefits of Pooled Regression?

The more data points there are, the higher the likelihood of accurately measuring an activity.
Naturally, when data is pooled, the number of data points increases.
This obviously will have positive consequences on the robustness of the model and the robustness of any measures. At the same time, it becomes possible to measure activities that take place at the regional level.

How Does Regional Modeling Work?

What happens behind the scenes is that all the data is pooled, and one single equation is estimated.
Let’s take the example of a product that is sold through three main accounts such as Boots, Asda, and Superdrug, which are three main retailers in the UK.
If for each store, there is data that stretches from the 1st of January 2020 to the 31st of December 2022, this gives exactly 152 data points for each account (retailer). If the analyst decides to pool the data, the size of the data set becomes: 152 x 3 = 456!
In other words, the number of data points tripled! This dataset expansion has different benefits that include:
The improvement of the robustness of the measure.
The ability to measure impact at the regional level.
The ability to capture more media granularity

In mathematical terms, what happens is the following:
x_i = \left[ \begin{matrix} \left[ \begin{matrix} x_{i1}(0) \\ \vdots \\ x_{i1}(N-1) \end{matrix} \right] \\ \vdots \\ \left[ \begin{matrix} x_{iK}(0) \\ \vdots \\ x_{iK}(N-1) \end{matrix} \right] \\ \end{matrix} \right]
\begin{matrix} \rightarrow \text{Unit 1} \ (e.g. \ \text{Region 1}) \\ \end{matrix}
\begin{matrix} \vdots \\ \end{matrix}
\begin{matrix} \rightarrow \text{Unit k} \ (e.g. \ \text{Region 2}) \\ \end{matrix}
x_i = \left[ \begin{matrix} \left[ \begin{matrix} x_{i1}(0) \\ \vdots \\ x_{i1}(N-1) \end{matrix} \right] \\ \vdots \\ \left[ \begin{matrix} x_{iK}(0) \\ \vdots \\ x_{iK}(N-1) \end{matrix} \right] \\ \end{matrix} \right]
→ Unit 1 (e.g. Region 1)
\begin{matrix} \vdots \\ \end{matrix}
→ Unit 2 (e.g. Region 2)
- The data that comes in from every single account would be stacked (Asda, Super Drug, and Boots). Then, the regression line is estimated through all those stacked regions using the normal OLS methodology.
Problems With Pooling Data
To be able to apply OLS, the stacked regions need to have the same average. However, this is not always the case. Sometimes, the analyst pools regions where there are high sales in some regions and low sales in others.
In such case, if no transformation is applied to the data and OLS is applied to non-transformed (or non-standardized) data, then:
in the regions where sales are lower than the average, sales will be overestimated by the model
in the regions where sales are above average, sales will be underestimated by the model.
- That’s why it is advisable to apply normalization to data to be able to use Pooled Regression and obtain meaningful results.
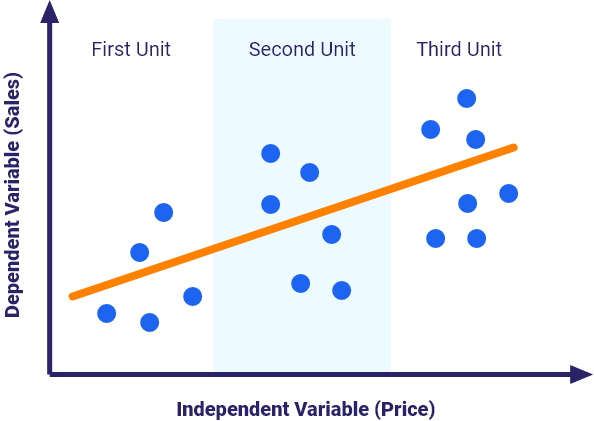
The following example depicts the relationship between price and sales at the level of different regions. If each region is considered separately, it is clear that when the price increases, sales decrease, and if the price decreases, sales increase.
However, if the data is pooled without any transformation, then a line is fitted through the six points seen in the charts, the relationship between price and sales becomes positive. And that is counter intuitive.
When is normalization needed?

If the intent behind pooling the data is analyzing the details of the regional variations, then in most cases data normalization is needed.
However, if log-linear modeling is used, there is no need to normalize the data, because it would have already been normalized through the log-linear transformation. The other case where data normalization is not needed is national models.
How could data be normalized?
There are many ways to normalize data. Amongst them we can cite:
- The mean is subtracted from the variable.
- The variable is divided by its mean.
- The variable is divided by the mean of the dependent variable.
When data is normalized in the context of Pooled Regression, the assumption is that the effect of the variable is the same across all the regions in percentage terms, which is a fair assumption to make.

Normalization in MassTer
This processor is very handy and is used during Pooled Regression. Estimating pooled data will allow reporting the average impact of each activity across all the fitted regions/cross sections. You can split one or multiple regions from the rest of the regions by using multiple selections.
- e.g. if the brand is running a national TV campaign, what is expected is that in percentage terms, the impact of the campaign is the same across the regions. Now, if that gets multiplied by the size of the region, the impact of TV will be more substantial in bigger regions which is what one would expect.
Sometimes, it is safe to suspect that some regions are more sensitive to activity than others. In that context, it is advisable to split the variable across the regions to measure different coefficients and hence different effects.
- e.g. if the analyst is modeling across north and south, and they think that customers in the south are more sensitive to prices, what they can do is split the price variable across north and south. This way, they can measure a different elasticity of price between the two regions.
As a rule of thumb, one should always assume the same percentage contribution across regions, but whenever we suspect that certain regions behave differently, we use the Splitter transformation to account for different elasticities of the marketing and media variable across the modeled regions.
Summary
Pooled Regression is a statistical technique used in Marketing Mix Modeling to account for differences at the regional level (by store, retailer, product, market, etc.). Regional data allows to enlarge the dataset to cover more data points, therefore increasing the robustness of all measures.
Pooled Regression (fixed effect) is estimated using Ordinary Least Squares (OLS). To apply pooled OLS, the regions need to have the same average. If they don’t, it is advised to perform normalization. However, that would not be needed if you use log-linear modeling, the topic of our next article!