Nested Modeling for Marketing Mix Modeling
Measuring Interaction Between Channels
Nested Modeling for Marketing Mix Modeling
Measuring Interaction Between Channels
Previously in the series, we explained the powerful uses of log-linear modeling. In this article, we learn about nested modeling, the advanced technique used to disentangle the impact of interactions between marketing channels.
When doing MMMs, you would ideally have each marketing variable influence sales separately: Search activity influences sales. TV influences sales etc. This assumes that there is no interaction between search and television. In real life, however, this is not the case.

To explain this with a practical example, let’s take the example of a Telco company. They are running a multichannel marketing campaign and want to measure their sales drivers.
Some of their customers buy the brand directly after being exposed to their TV campaign. In this case, we would attribute the sales impact to the TV campaign.

Other customers would search for the brand after seeing the TV ad and then decide to buy.
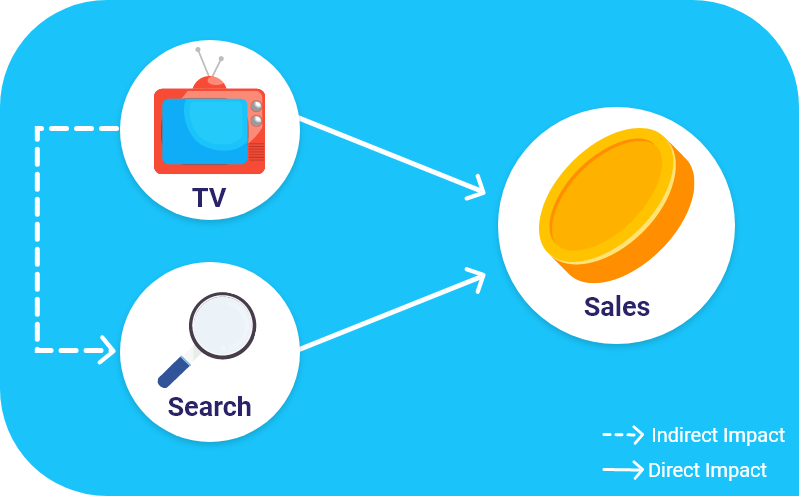
Based on last touchpoint attribution, the sales conversion would count as part of the search channel. However, the TV campaign has clearly had an impact! The search activity that had led to purchase probably wouldn’t have happened without it.
Clearly, the indirect impact of TV should be accounted for when computing the total contribution of the TV campaign. But how? It is very difficult to measure this interaction with traditional modeling approaches.
In Regression Analysis, the go-to method for estimating unknown parameters is Ordinary Least Squares (OLS). However, if the analyst wants to use OLS, they should assume that the explanatory variables are independent from the error term. The trouble is that in the context of the example explained above, the regressors have a correlation with the error term. This is called the endogeneity problem. Because of this problem, the OLS estimation cannot be used.

What Makes Nested Models Special
Nested modeling presents many benefits. The most important of which is the fact that it allows measuring both the direct and indirect impact of every single channel. Thus, it is possible to adjust contribution and ROI to reflect the full contribution of every single media and marketing variable.
The graph below depicts different relationships between the different media channels and all those relationships are taken into consideration when estimating the main model. OLS fails to do this and the method that should be used here is the 2SLS method.

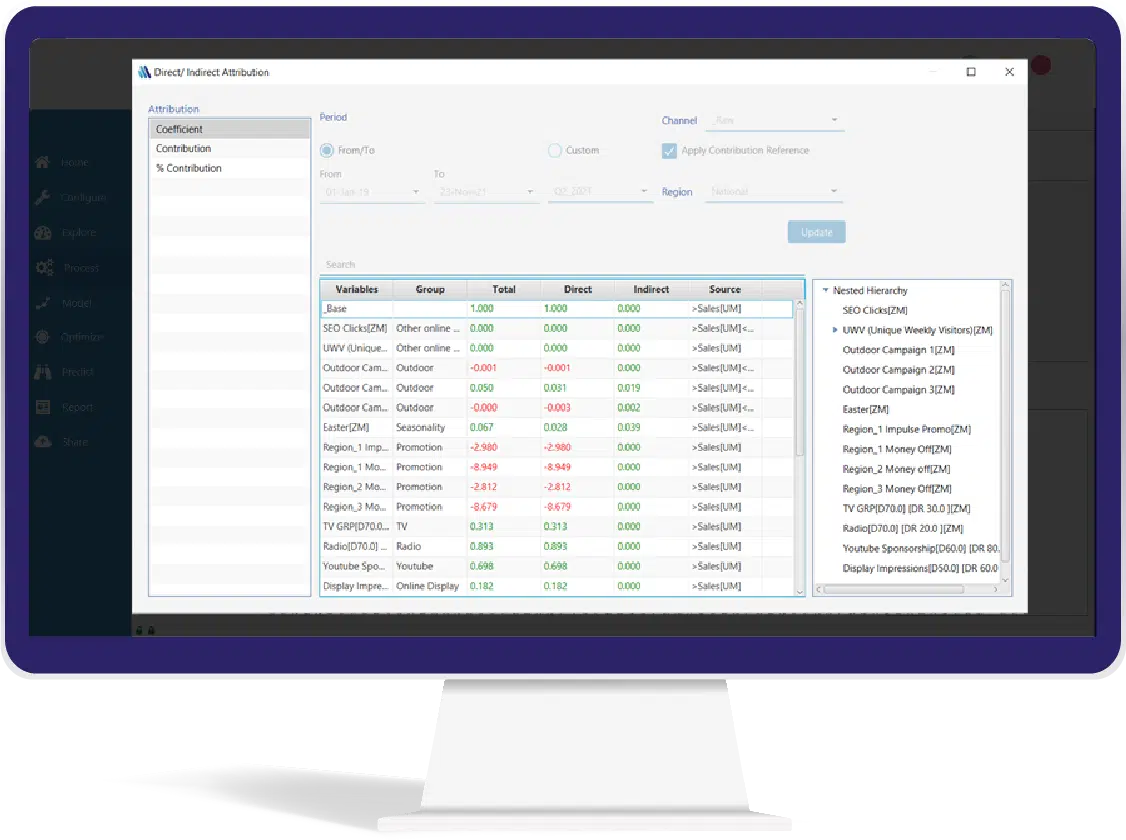
Direct/Indirect Attribution
Use this screen in your MMM tool MassTer, to display the direct, indirect, and total impact of all included variables in the nested model.
How 2SLS Works?
Let’s say we have two equations. The first equation is the main equation. For example, sales are influenced by search and TV. We’ll consider this as the main model:
y=b_{0}+Xb+\beta \widehat{z}
The second equation is Search. It is influenced by TV and other variables. This is called the reduced model, or sometimes the secondary model:
\widehat{z}=c_{0}+TVc
To build a nested model, follow these steps:
First, estimate the secondary model and derive the coefficients’ estimates.
Then, plug that equation into the main model to estimate both the direct and indirect impact.
y=b_{0}+Xb+\beta \widehat{z}
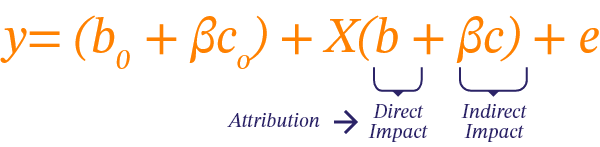
If there is a variable that only appears in the main model, it will only have a direct impact.
However, if it appears in both, then it will have a direct impact on the main model and an indirect impact through it is impact on the secondary model.
Conclusion
You cannot assume that there is no interaction between the channels of a campaign, considering the interactive nature of the world in which we live. Acknowledging that interaction by using appropriate methods, like nested models, will allow you to measure the direct and indirect impact of each channel.
Assuming there is no interaction between channels is not realistic. With nested modeling, you can represent that relationship. It works by integrating the different interactions into the main model, allowing you to measure the direct and indirect impact of each channel. Satisfied with your model’s performance?
It’s time to optimize!